여기서는 LP(linear programming) problem의 예제들을 보며 그것들을 어떻게 푸는지를 다룬다.
문제 :
Maximize 3x + 4y subject to the following connstraints:
1. x + 2y ≤ 14
2. 3x - y ≥ 0
3. x - y ≤ 2
위 문제에서의 objective function과 constraint들은 linear expression으로 표현되어있다.
(즉 linear problem)
constraint는 feasible region으로 선언되어있으며, 아래 그림과 같다.

Basic steps for solving an LP problem
1. import the linear solver wrapper
2. declare the LP solver
3. define the variables
4. define the constraints
5. define the objective
6. call the LP solver
7. display the solution
(wrapper를 import하고 LP solver를 선언. 그리고 변수와 constraint값, 그리고 objective를 선언한 후 LP solver 호출)
Solution using the MPSolver
여기서는 MPSolver wrapper과 LP solver를 사용할 예정이므로 OR-Tools 설치가 필요하다.
주요 OR-Tools linear optimization solver는 Glop이며 이는 google's in-house linear programming solver이다.
(이는 빠르고 메모리에도 효율적이며 수치적으로도 안정적이다)
1. Import the linear solver wrapper
#import OR-Tools linear solver wrapper
from ortools.linear_solver import pywraplp2. Declare the LP solver
MPsolver는 Glop를 포함한 여러 다른 solver들을 위한 wrapper이다.
#the code below declares the GLOP solver
solver = pywraplp.Solver.CreateSolver('GLOP')
if not solver:
returnGLOP대신 PDLP를 사용해도된다.
더 다양한 solver를 보고자 한다면 advanced LP solving를 참고하라. (다음 포스트에서 공부할 예정)
3. Create the variables
0부터 inf까지 범위에 있는 값으로 x, y 변수를 만들어야 한다.
x = solver.NumVar(0, solver.infinity(), 'x')
y = solver.NumVar(0, solver.infinity(), 'y')
print('Number of variables = ', solver.NumVariables())4. Define the constraints
다음으로 선언한 변수에 기반하여 constraint를 정의한다. 각 constraint 별로 넘버링을 하였으며 constraint에 대한 상수들을 선언하였다.
# constraint0 : x + 2y <= 14
solver.Add(x + 2 * y <= 14.0)
# constraint 1 : 3x - y >= 0
solver.Add(3 * x - y >= 0.0)
# constraint 2 : x - y <= 2
solver.Add(x - y <= 2.0)
print('Number of constraints = ', solver.NumConstraints())5. Define the objective function
objective function을 선언하고, 이 문제가 maximization problem임을 특정한다.
# Objective function : 3x + 4y
solver.Maximize(3 * x + 4 * y)6. Invoke the solver
status = solver.Solve()7. Display the soultion
if status == pywraplp.Solver.OPTIMMAL:
print('Solution:')
print('Objective value = ', solver.Objective().Value())
print('x = ', x.solution_value())
print('y = ', y.solution_value())
else:
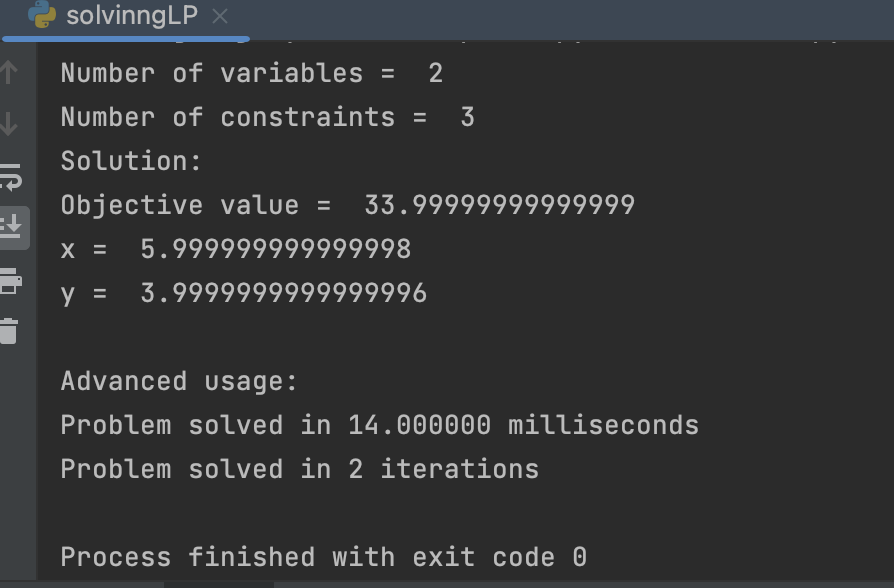
print('The problem does not have an optimal solution.')pycharm 실행 결과 :

reference :
https://developers.google.com/optimization/lp/lp_example
LP 문제 해결 | OR-Tools | Google Developers
이 페이지는 Cloud Translation API를 통해 번역되었습니다. Switch to English 의견 보내기 LP 문제 해결 컬렉션을 사용해 정리하기 내 환경설정을 기준으로 콘텐츠를 저장하고 분류하세요. 다음 섹션에서
developers.google.com
'M.S. > OR-Tools' 카테고리의 다른 글
| [OR-Tools 스터디] Solving a MIP Problem (0) | 2023.02.13 |
|---|---|
| [OR-Tools 스터디] Integer Optimization (Overview) (0) | 2023.02.13 |
| [OR-Tools 스터디] The Stigler Diet Problem (0) | 2023.02.08 |
| [OR-Tools 스터디] Linear Optimization (0) | 2023.02.07 |
| [OR-Tools 스터디] About OR-Tools (0) | 2023.02.07 |


댓글